Math

L1. Functions of sevral variables

画等高线图

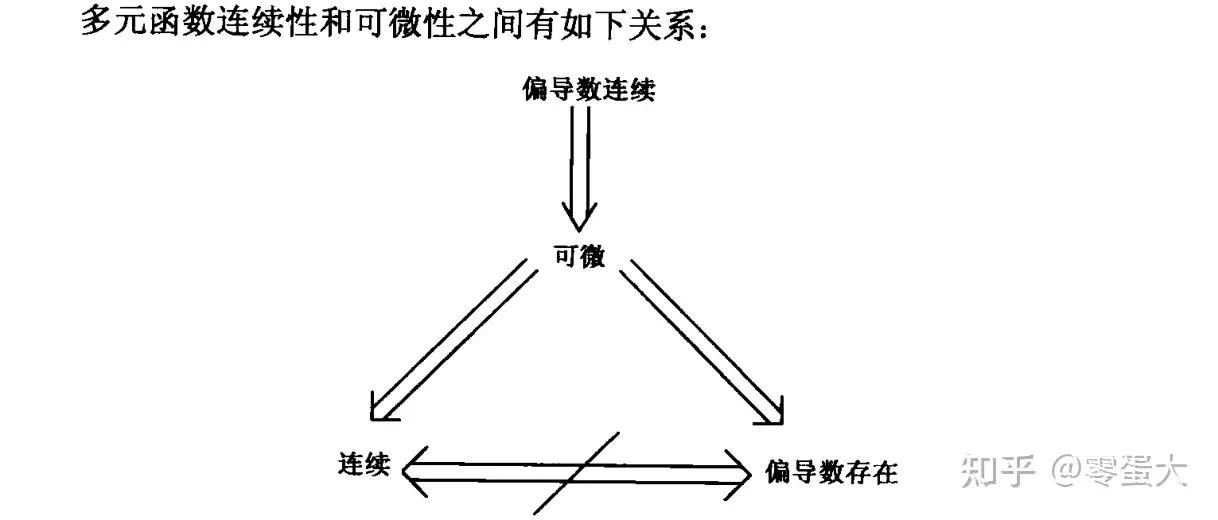
L2. Limits and continuity

极限

定义：对于一个二元函数f，在点(a, b)处的极限L意味着当(x, y)无限接近于(a, b)时，f(x, y)无限接近于L。这个极限必须对所有可能接近(a, b)的方向都成立。

例如证明$\lim_{(x,y)\to(0,0)}\frac{x^3}{x^2+y^2}$不存在,可以考虑使用$y=kx$，$y=kx^2$来进行逼近，同时可以考虑使用极坐标法来进行换元

连续性

定义：如果$\lim_{(x,y)\to(a,b)}f(x,y)=f(a,b)$，则称函数f在点(a, b)处是连续的。若f在定义域D中的每一点都是连续的，则称f在D上是连续的。

例如证明$f(x,y)=\frac{x^2}{x^2+y^2}$在$(x,y)=(0,0)$点不连续，只要证明在$(x,y)=(0,0)$这个点上$\lim_{(x,y)\to(a,b)}f(x,y) \neq f(a,b)$

当然$\lim_{(x,y)\to(0,0)}\frac{x^3}{x^2+y^2}$不存在，所以$\lim_{(x,y)\to(a,b)}f(x,y) \neq f(a,b)$成立

L3. Partial derivatives

定义：对于二元函数$f(x,y)$，它的偏导数是关于$x$或$y$的函数，即分别固定$y$或$x$，然后对另一个变量求导。
符号：偏导数使用符号$\frac\partial{\partial x}$或$\frac\partial{\partial y}$示。

设$f(x, y) = e^{x^2 + y^2}$，求$f_{xx}(x, y)$和$f_{yy}(x, y)$。

首先计算一阶偏导数$f_x = 2xe^{x^2 + y^2}$和$f_y = 2ye^{x^2 + y^2}$，接着再求各自的偏导数，得到$f_{xx} = 2e^{x^2 + y^2} + 4x^2e^{x^2 + y^2}$和$f_{yy} = 2e^{x^2 + y^2} + 4y^2e^{x^2 + y^2}$。

L4. Tangent Planes and Linear approximations

切平面：

对于二元函数f(x, y)，其在点(a, b)附近的良好近似是由z=f(x, y)在点P(a, b, c=f(a, b))处的切平面给出的。

如果f有连续的偏导数，则过点P(a, b, c)的切平面方程为：$z-c = f_x(a,b)(x-a) + f_y(a,b)(y-b)$。

线性近似：

线性近似提供了一种几何方法，用于获取二元函数在其定义域中某点$(a, b)$附近的良好近似。
线性化L(x, y)是在点(a, b)处对函数f的线性逼近，表达式为$L(x,y)=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)$。

可微函数：

L5. The chain rules

链式法则：

假设$z=f(x,y)$，而x和y都依赖于一个参数$t$，即$x=x(t)$，$y=y(t)$，通过链式法则计算$z$关于$t$的变化率，公式为：

$\frac{df}{dt} = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt}$

假设$z=f(x,y)$，其中$x$和$y$依赖于两个参数$s$和$t$，即$x=x(s,t)$，$y=y(s,t)$，通过链式法则计算$z$关于$s$和$t$的偏导数，公式分别为：

$\frac{\partial f}{\partial s} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial s}$

$\frac{\partial f}{\partial t} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t}$

隐函数微分：

例如要求一个隐函数中$z$对$x$的偏导

对其应用$\frac{\partial F}{\partial x}\frac{\partial x}{\partial x}+\frac{\partial F}{\partial y}\frac{\partial y}{\partial x}+\frac{\partial F}{\partial z}\frac{\partial z}{\partial x} = 0$

例如给定的方程是：$x^2z + y^3 + z^2 = 2$

对方程两边关于 (x) 求偏导，得到：

$\frac{\partial}{\partial x}(x^2z) + \frac{\partial}{\partial x}(y^3) + \frac{\partial}{\partial x}(z^2) = \frac{\partial}{\partial x}(2)$

计算每一项：

对$x^2z$使用乘积法则求导：$\frac{\partial}{\partial x}(x^2z) = 2xz + x^2\frac{\partial z}{\partial x}$（这里$x$，$z$不是无关项，得应用乘积法则求导）
2.$y^3$是一个与$x$无关的常数，所以它的偏导是 0。
对$z^2$使用链式法则求导：$\frac{\partial}{\partial x}(z^2) = 2z\frac{\partial z}{\partial x}$
右边是一个常数，其偏导为 0。

因此，我们有：

$2xz + x^2\frac{\partial z}{\partial x} + 2z\frac{\partial z}{\partial x} = 0$

整理得：

$x^2\frac{\partial z}{\partial x} + 2z\frac{\partial z}{\partial x} = -2xz$

提取公因式$\frac{\partial z}{\partial x}$得到：

$\frac{\partial z}{\partial x}(x^2 + 2z) = -2xz$

最后，解出$\frac{\partial z}{\partial x}$：

$\frac{\partial z}{\partial x} = \frac{-2xz}{x^2 + 2z}$

L6. Directional derivatives and the gradient vector

方向导数

定义：方向导数是函数在某一点沿特定方向的变化率，其方向为上升最快的方向

公式：如果$f$是一个可微函数，则$f$在单位向量$\mathbf{u} = \langle a, b \rangle$方向上的方向导数为：

$D_{\mathbf{u}} f(x, y) = \nabla f(x, y) \cdot \mathbf{u}$

例如设$f(x, y) = x^2 + y^2$，求在点(1, 1)处沿向量$\mathbf{u} = \left\langle \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right\rangle$的方向导数。

先计算梯度$\nabla f = \langle 2x, 2y \rangle$，然后代入点(1, 1)得到$\nabla f(1, 1) = \langle 2, 2 \rangle$。接下来计算点积$\langle 2, 2 \rangle \cdot \left\langle \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right\rangle = 2\sqrt{2}$。

L7. maximum and minimum

临界点

定义：临界点是使得梯度为零的点，或者至少有一个偏导数不存在的点。

例如找出函数$f(x, y) = x^2 + y^2$的临界点，并判断它是否对应于局部极值。

由于$f(x, y) \geq f(0, 0) = 0$，并且$\nabla f = \langle 2x, 2y \rangle$，唯一的临界点是$(0, 0)$，这确实是一个局部极小值点。

例如找出函数$f(x, y) = x^2 - y^2$的临界点，并判断它是否对应于局部极值。

临界点依然是$(0, 0)$，但是在这个点附近，我们可以找到比$f(0, 0)$更大和更小的值，因此这不是一个局部极值点，而是一个鞍点。

第二导数测试

对于临界点$(a, b)$，通过计算二阶偏导数可以使用第二导数测试来确定该点是否为局部极值或鞍点。

测试基于判别式$D = f_{xx}(a,b)f_{yy}(a,b) - [f_{xy}(a,b)]^2$：

如果$D>0$且$f_{xx}(a,b)>0$，则$(a, b)$是局部极小值；
如果$D>0$且$f_{xx}(a,b)<0$，则$(a, b)$是局部极大值；
如果$D<0$，则$(a, b)$是鞍点；
如果$D=0$，则测试无效，需要其他方法进一步分析。

全局极值

对于连续函数$f$在闭合有界集$D$上，$f$必定取得全局最大值和最小值，这些值可能出现在临界点或边界上。

找到全局极值的方法包括：

寻找$D$内所有临界点处的函数值；
确定$D$边界上的极值；
比较上述两步得到的所有值，其中最大者为全局最大值，最小者为全局最小值。

例如求函数$f(x, y) = 3x - x^3 - 2y^2 + y^4$在$x \geq 0$的局部极大值、极小值和鞍点。

计算一阶偏导数：
$f_x = 3 - 3x^2, \quad f_y = -4y + 4y^3$

计算二阶偏导数：
$f_{xx} = -6x, \quad f_{yy} = -4 + 12y^2, \quad f_{xy} = 0$

计算判别式$D$：
$D = f_{xx}f_{yy} - (f_{xy})^2 = (-6x)(-4 + 12y^2) = 24x(1 - 3y^2)$

确定可能的驻点：
驻点满足$\nabla f = <3 - 3x^2, -4y + 4y^3> = <0, 0>$，解得：
$x = \pm 1, \quad y = 0, \quad \pm 1$

分析每个驻点：

对于点$(1, 0)$：
$$
f_{xx}(1, 0) = -6<0, \quad D = 24(1 - 3 \cdot 0^2) = 24>0
$$
根据二阶导数测试，$(1, 0)$是一个局部极大值。
对于点$(1, 1)$和$(1, -1)$

$$
f_{xx}(1, \pm 1) = -6<0, \quad D = 24(1 - 3 \cdot (\pm 1)^2) = -48<0
$$

根据二阶导数测试，$(1, 1)$和$(1, -1)$是鞍点。
对于点$(-1, 0)$

$$
f_{xx}(-1, 0) = 6>0, \quad D = -24(1 - 3 \cdot 0^2) = -24<0
$$

根据二阶导数测试，$(-1, 0)$是鞍点。
对于点$(-1, 1)$和$(-1, -1)$

$$
f_{xx}(-1, \pm 1) = 6>0, \quad D = -24(1 - 3 \cdot (\pm 1)^2) = 48>0
$$

根据二阶导数测试，$(-1, 1)$和$(-1, -1)$是局部极小值点。

L8. Lagrange Multiplier

拉格朗日乘数法

沿指定曲线在$f$的定义域内寻找$f(x,y)$的极小值和极大值，即在给定约束条件下最大化或最小化$f$

例如找到长度为9的3D向量，其中包含其分量的最大可能乘积

约束条件是向量的长度必须等于9：

$\sqrt{x^2 + y^2 + z^2} = 9$即$x^2 + y^2 + z^2 = 81$

设置拉格朗日函数

$\mathcal{L}(x, y, z, \lambda) = xyz - \lambda (x^2 + y^2 + z^2 - 81)$

然后对$x$,$y$,$z$和$\lambda$求偏导数，并令它们等于零：

$\frac{\partial \mathcal{L}}{\partial x} = yz - 2\lambda x = 0$

$\frac{\partial \mathcal{L}}{\partial y} = xz - 2\lambda y = 0$

$\frac{\partial \mathcal{L}}{\partial z} = xy - 2\lambda z = 0$

$\frac{\partial \mathcal{L}}{\partial \lambda} = -(x^2 + y^2 + z^2 - 81) = 0$

然后求解出$x$,$y$,$z$和$\lambda$的值

L9. Sequences

求解数列的极限

对于数列$a_n=\frac{7n^2+5n-3}{6n^2-4}$,通过应用极限的性质计算得出$\lim_{n\to\infty}a_n=\frac76$

夹逼定理

例如证明${c_n} = { (-1)^n \frac{1}{n!} }$收敛

因为在$n$趋于无穷的时候$\frac1{n!}$趋近于0，对$-\frac1{n!}$同理

$-\frac1{n!}\leq(-1)^n\frac1{n!}\leq\frac1{n!}$

所以${c_n}$收敛

L10 Series

几何级数 (Geometric Series)

几何级数的形式为$\sum ar^{n-1}$，其中$r$是比值。

当$|r|<1$时，几何级数收敛，其和为$\frac{a}{1-r}$；当$|r| \geq 1$时，几何级数发散。

第$n$项判别法 (n-th term test for divergence)

如果级数$\sum a_n$收敛，则$\lim_{n \to \infty} a_n = 0$。反之，如果$\lim_{n \to \infty} a_n \neq 0$，则级数必定发散。

注意，$\lim_{n \to \infty} a_n = 0$并不是级数收敛的充分条件。

L11. Convergence tests for all series

绝对收敛 vs 条件收敛：对于含有正负项的级数，可以通过比较测试等方法来判断其是否绝对收敛。如果级数绝对收敛，那么它可以被重新排列而不影响其收敛性或和。条件收敛的级数则不一定具有此性质。

交错级数测试（Leibniz's Test）：用于判断交错级数的收敛性。交错级数是指符号在正负之间交替变化的级数。例如，$\sum_{n=1}^{\infty} (-1)^{n+1} / n$是一个交错级数。该测试要求级数满足两个条件：(a) 绝对值逐渐减小，(b) 极限为0。

p-级数测试：形式为$\sum 1/n^p$，其中$p$是一个常数。若$p>1$，则级数收敛；若$p \leq 1$，则级数发散。

L12. Convergence tests for postive series

收敛测试方法

比较测试（Comparison Test）

比较测试是通过与已知收敛或发散的级数进行比较来判断一个级数是否收敛的方法。例如：

例如考虑级数$\sum \frac{1}{n!}$。

对于$n>3$，我们知道$2^n<n!$，因此$\sum \frac{1}{2^n}>\sum \frac{1}{n!}$。由于几何级数$\sum \frac{1}{2^n}$收敛，所以由比较测试可知$\sum \frac{1}{n!}$也收敛。
积分测试（Integral Test）

积分测试适用于连续、正且非增函数$f(x)$的级数。如果对应的反常积分$\int f(x) dx$收敛，则级数$\sum f(n)$也收敛。例如：

例如考虑级数$\sum \frac{1}{x^2 \ln(x)}$。

设$f(x) = \frac{1}{x^2 \ln(x)}$，计算得到$\int_2^\infty \frac{1}{x^2 \ln(x)} dx = -\frac{1}{\ln(x)}\Big|_2^\infty = \ln(2)$。因为积分收敛，所以根据积分测试，该级数收敛。
P-级数测试（P-Series Test）

P-级数是指形如$\sum \frac{1}{n^p}$的级数，其中$p$是常数。P-级数在$p>1$时收敛，在$p \leq 1$时发散。

例如$\sum\frac1{n^2}\cos\left(\frac1{n^2}\right)$，可以考虑使用p-级数$\sum\frac1{n^2}$因为$\cos\left(\frac1{n^2}\right)< 1$,所以$\frac1{n^2}\cos\left(\frac1{n^2}\right)<\frac1{n^2}$，故收敛

特例：调和级数$\sum \frac{1}{n}$发散
极限比较测试（Limit Comparison Test）

极限比较测试是改进后的比较测试，允许忽略小项。例如，有两个正项级数$\sum a_n$和$\sum b_n$，并且$\lim_{n\to\infty} \frac{a_n}{b_n} = L$，其中$0<L<\infty$，则两个级数要么都收敛，要么都发散。

例如$\sum a_n = \sum \frac{3n^2 + 2n + 1}{n^3 + 1}$的收敛性。选择已知发散的调和级数$\sum b_n = \sum \frac{1}{n}$进行比较。

计算比值$\frac{a_n}{b_n}$并取极限：

$\lim_{n \to \infty} \frac{a_n}{b_n} = \lim_{n \to \infty} \frac{3n^3 + 2n^2 + n}{n^3 + 1} = \lim_{n \to \infty} \frac{3 + \frac{2}{n} + \frac{1}{n^2}}{1 + \frac{1}{n^3}} = 3$，$0<3<\infty$满足条件，发散
比值测试（Ratio Test）

当级数包含阶乘或幂次时，通常可以使用比值测试。这些测试对于处理含有$n!$或$n^n$这样的项特别有用。

例如$\sum_{n=1}^\infty\frac{7^n}{n!}$，计算$\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|$，得到：

$\lim_{n\to\infty}\left|\frac{\frac{7^{n+1}}{(n+1)!}}{\frac{7^n}{n!}}\right|=\lim_{n\to\infty}\left|\frac{7^{n+1}\cdot n!}{7^n\cdot(n+1)!}\right|=\lim_{n\to\infty}\left|\frac7{n+1}\right|=0$

由于极限值为0，小于1，因此级数收敛。
根测试（Root Test）

设有一个正项级数$\sum_{n=1}^{\infty} a_n$，其中$a_n>0$对所有$n$成立。定义：

$L = \limsup_{n \to \infty} \sqrt[n]{|a_n|}$

这里使用了上极限（$\limsup$）的概念，这是因为有时极限可能不存在，但是上极限总是存在的。根据$L$的值，可以得出以下结论：

如果$L<1$，那么级数绝对收敛。

如果$L>1$或$L = +\infty$，那么级数发散。

如果$L = 1$，根值测试无法给出关于级数收敛或发散的确切信息，这时需要采用其他测试方法。
第$n$项判别法 (n-th term test for divergence)

如果级数$\sum a_n$收敛，则$\lim_{n \to \infty} a_n = 0$。反之，如果$\lim_{n \to \infty} a_n \neq 0$，则级数必定发散。

L13. The Power series

幂级数的定义：

幂级数是一类形式为$\sum_{n=0}^{\infty} a_n x^n$的无穷多项式，其中$a_n$称为系数。
一个中心在$c$的幂级数的一般形式是$\sum_{k=0}^{\infty} a_k (x-c)^k$。

例如：

找到幂级数$\sum_{n=0}^{\infty} (-1)^n \frac{x^{2n}}{(2n)!}$的收敛区间。

使用比值测试法（Ratio Test），得到该幂级数对所有$x$都绝对收敛，因此其收敛区间为$(-∞, +∞)$。

找到幂级数$\sum_{n=1}^{\infty} \frac{(x-3)^n}{2^n}$的收敛区间。

同样使用比值测试法，得出$|x-3|<2$，即$1<x<5$。再测试端点$x=5$和$x=1$，发现两个端点处级数都发散，所以收敛区间为$(1, 5)$。

Note

注意测试边界

L14. The Taylor series

泰勒级数

$f(x) = f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + ···$

当$a=0$时，为麦克劳林级数